https://www.acmicpc.net/problem/5527
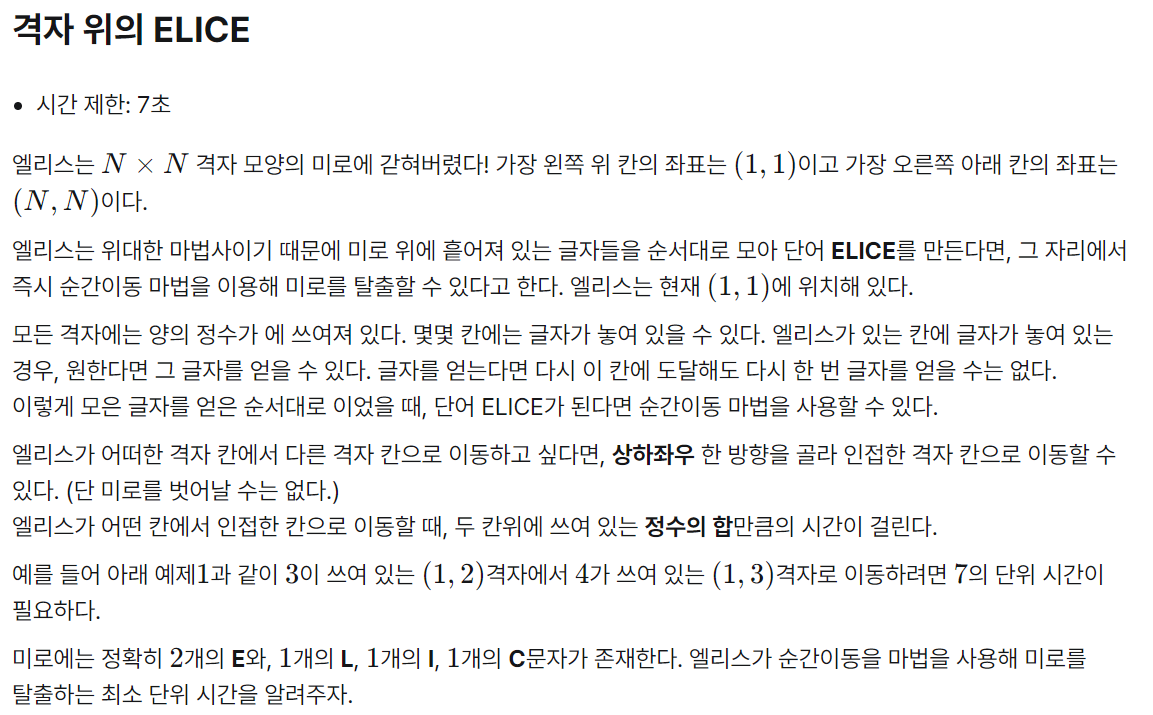
특정 범위의 전구 상태를 뒤집는 기계를 1번만 사용하여 연속된 교대 패턴의 최대 크기를 구하는 문제입니다.
교대 패턴은 말 그대로 인접한 전구의 상태가 다른 패턴입니다. 1 0 1 0 1 이나 0 1 0 1같은 패턴입니다.
dp를 활용하여 특정 범위를 뒤집으면서 할 수도 있겠지만 다른 방법으로 쉽게 풀렸습니다.
1 1 0 0 1 0 1 1 1 0입력이 이렇게 주어졌을때 각 교대패턴의 크기를 구하면
1 2 4 1 2 이렇게 됩니다.
그렇다면 여기서 한 구간을 뒤집게 되면 왼쪽과 오른쪽에 인접한 구간과 하나의 패턴으로 합쳐질 수 있습니다.
각 교대 패턴이 1 0 / 0 1 0 1 / 1
이렇게 되어있다고 했을때 0 1 0 1을 뒤집어주면 1 0 1 0이 됩니다.
그러면 전구들의 상태는 1 0 / 1 0 1 0 / 1 이렇게 되므로 세 구간은 하나로 합쳐지고, 크기는 7이 됩니다.
즉 연속된 3개 패턴 크기의 합의 최댓값을 구해주시면 답을 구하실 수 있습니다.
물론 패턴의 갯수가 3개보다 작으면 그 패턴 크기의 합을 구해주시면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
#include <iostream>
#include <vector>
#define MAX 100001
using namespace std;
vector<int> v;
int list[MAX];
int N;
void init() {
int pre = list[0];
int cnt = 1;
for (int i = 1; i < N; i++) {
if (pre == list[i]) {
v.push_back(cnt);
cnt = 1;
}
else {
cnt++;
}
pre = list[i];
}
v.push_back(cnt);
}
void func() {
init();
int ret = 0;
if (v.size() < 3) {
for (auto x : v) {
ret += x;
}
}
else {
for (int i = 1; i < v.size() - 1; i++) {
ret = max(ret, v[i - 1] + v[i] + v[i + 1]);
}
}
cout << ret << '\n';
}
void input() {
cin >> N;
for (int i = 0; i < N; i++) {
cin >> list[i];
}
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
return 0;
}
|
cs |
'algorithm > ad-hoc' 카테고리의 다른 글
| boj 21316 스피카 (0) | 2024.08.05 |
|---|---|
| boj 10350 Banks (0) | 2024.07.31 |
| boj 14864 줄서기 (0) | 2024.07.26 |
| boj 2381 최대 거리 (0) | 2024.07.25 |
| boj 14675 단절점과 단절선 (0) | 2024.07.23 |