https://www.acmicpc.net/problem/27966
N개의 정점으로 이루어진 트리에서 i < j인 정점들 사이 거리가 최소가 되도록 하려면 어떤 트리를 만들어야하는지 구하는 문제입니다.
트리를 직접 그려보면 Star Graph 형식이 최소가 된다는 것을 알 수 있습니다.
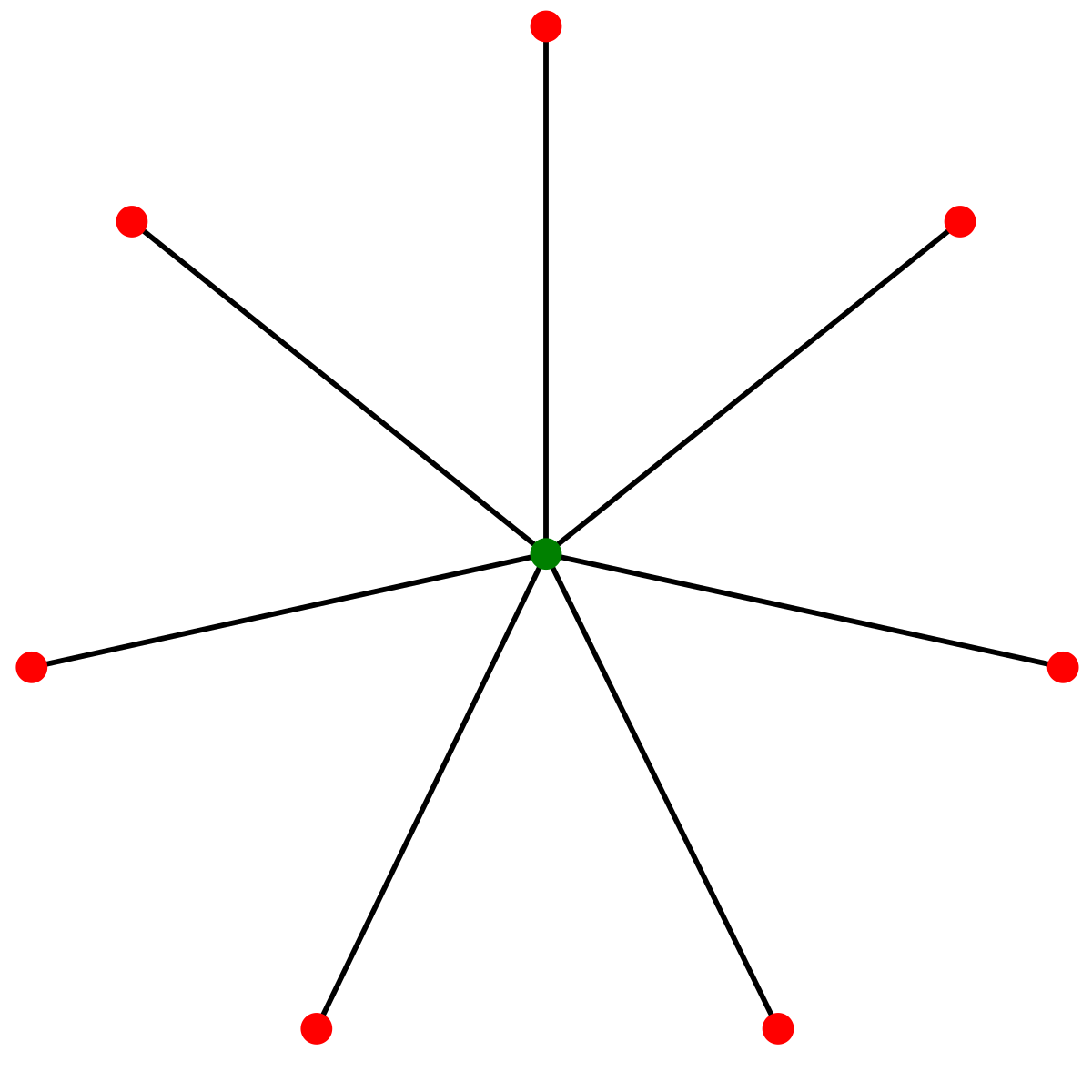
Star Graph는 하나의 정점에 다른 모든 정점이 연결된 형태입니다.
이렇게되면 1번 정점과 연결된 다른 정점은 거리가 각각 1입니다. (N - 1)
나머지 정점들끼리의 거리는 각각 2입니다.
나머지 N - 1개의 정점에서 2개를 고르는 경우의 수는 N-1C2이며, 두개 곱하면 (N - 2) * (N - 1)이 됩니다.
위에서 구한 두 수를 더하면 N - 1 + (N - 2) * (N - 1) 이라는 답을 구할 수 있습니다.
스페셜 저지 문제이기 때문에 기준이 되는 정점을 아무거나 고르시면 됩니다. 저는 1번 정점을 기준으로 정했습니다.
그리고 기준이 되는 정점과 i를 반복해서 출력해주시면 되겠습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
#include <iostream>
using namespace std;
typedef long long ll;
ll N;
void func() {
cout << N - 1LL + (N - 2LL) * (N - 1LL) << '\n';
for (int i = 2; i <= N; i++) {
cout << "1 " << i << '\n';
}
}
void input() {
cin >> N;
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
return 0;
}
|
cs |
'algorithm > ad-hoc' 카테고리의 다른 글
| boj 7982 순열 그래프의 연결성 판별 (0) | 2024.08.16 |
|---|---|
| boj 16161 가장 긴 증가하는 팰린드롬 부분수열 (0) | 2024.08.15 |
| boj 24553 팰린드롬 게임 (0) | 2024.08.07 |
| boj 14370 전화번호 수수께끼 (Large) (0) | 2024.08.06 |
| boj 21316 스피카 (0) | 2024.08.05 |
