문제

풀이
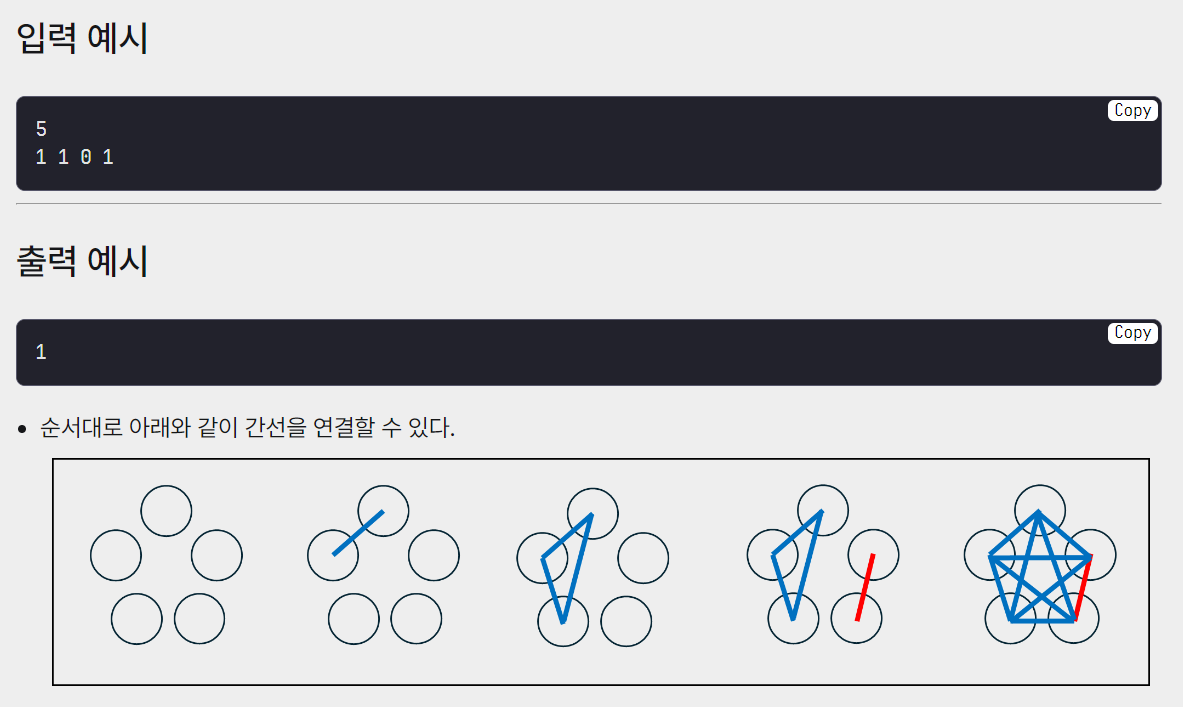
입력에는 빨간 간선인지, 파란 간선인지 주어집니다.
그러면 정점 2개를 골라서 각 정점이 포함된 연결 요소의 모든 정점들을 서로 연결시켜줍니다.
이때 사용되는 간선들 중 빨간 간선의 갯수가 최소가 되도록 정점을 적절하게 골라야 합니다.
처음에는 그냥 연결된 간선이 적은 정점 2개를 골라주면 되는것 아닌가? 라는 생각이 들었었고,
우선순위 큐를 이용하여 작은 값 2개의 합을 더해주는 방식으로 구현했더니 60점이 나왔었습니다.
이 방법이 맞다면 반례가 없을텐데 정답이 아닌걸로 봐서 제가 접근한 방식이 틀린거였습니다.
문제의 솔루션은 bfs + map을 사용하는 것이었습니다.
배열에는 각 연결요소에 포함된 정점의 갯수를 저장합니다.
N이 5라고 가정하면 처음에는 1 1 1 1 1이 배열에 저장됩니다.
그리고 이 배열의 상태를 방문처리 합니다.
그 다음 bfs를 통해 각 연결요소들을 2개씩 뽑아서 연결합니다.
이때 배열을 정렬해줘야 방문처리를 할 수 있습니다.
각 연결요소의 크기가 1 1 2 2인 것과 2 1 2 1인 것 둘다 똑같은 결과가 나옵니다.
그리고 그 간선이 빨간 간선일 때만 갯수를 세어줍니다.
해당 연결요소들의 상태가 map에 없을때만 queue에 넣어주고, map에 있을때는 최솟값을 갱신해주도록 합니다.
모든 정점이 연결되면 연결요소의 상태가 {N}이 되며, 이를 map에서 꺼내면 답을 구할 수 있습니다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#define MAX 31
using namespace std;
int list[MAX];
int N;
int bfs() {
vector<int> v = vector<int>(N, 1);
map<vector<int>, int> m;
m[v] = 0;
queue<vector<int> > q;
q.push(v);
for (int t = 0; t < N - 1; t++) {
int qsize = q.size();
while (qsize--) {
auto x = q.front();
q.pop();
int size = x.size();
for (int i = 0; i < size - 1; i++) {
for (int j = i + 1; j < size; j++) {
vector<int> tmp;
for (int k = 0; k < size; k++) {
if (i == k || j == k) continue;
tmp.push_back(x[k]);
}
tmp.push_back(x[i] + x[j]);
sort(tmp.begin(), tmp.end());
if (m.find(tmp) == m.end()) {
q.push(tmp);
if (!list[t]) m[tmp] = m[x] + x[i] * x[j];
else m[tmp] = m[x];
}
else {
if (!list[t]) m[tmp] = min(m[tmp], m[x] + x[i] * x[j]);
else m[tmp] = min(m[tmp], m[x]);
}
}
}
}
}
return m[{N}];
}
void func() {
cout << bfs() << '\n';
}
void input() {
cin >> N;
for (int i = 0; i < N - 1; i++) {
cin >> list[i];
}
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
return 0;
}
|
cs |
'대회 > elice' 카테고리의 다른 글
| 엘리스 코드 챌린지 Day 8 강림제 (0) | 2024.07.23 |
|---|---|
| 엘리스 코드 챌린지 Day 7 계기판 조작하기 (0) | 2024.07.23 |
| 엘리스 코드 챌린지 Day 5 수열 복원 (0) | 2024.07.22 |
| 엘리스 코드 챌린지 Day 4 트리 위의 게임 (0) | 2024.07.22 |
| 엘리스 코드 챌린지 Day 3 문자열 압축 해제 (4) | 2024.07.22 |