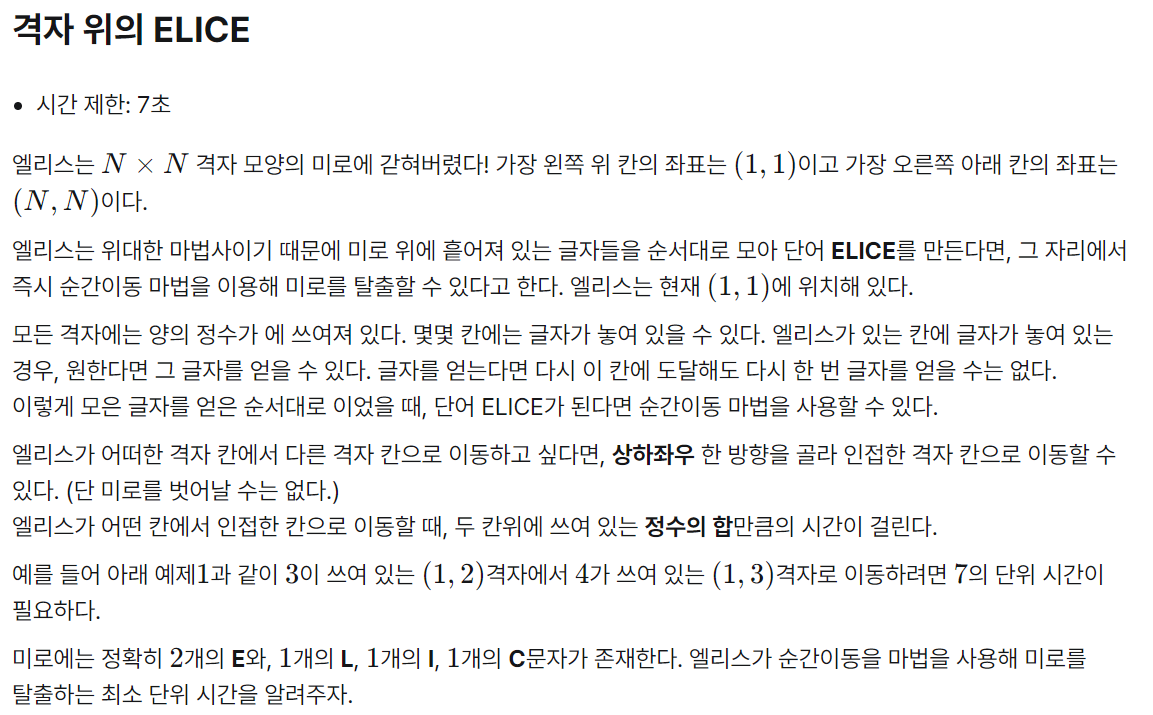
문제

풀이
(1, 1)에서 출발하여 E L I C E를 한글자씩 순서대로 모두 모을 수 있는 최소 거리를 구하는 문제입니다.
여기서 E는 2개의 위치가 주어지지만 동일한 글자로 취급하기 때문에 어떤 곳을 먼저가도 상관 없습니다.
어떻게하면 더 효율적으로 구할 수 있는지 생각해봤지만 다익스트라로 간단하게 구할 수 있는 문제였습니다.
저는 우선 ELICE에 해당하는 글자들의 좌표를 한 배열에 넣고, 출발 지점인 (1, 1)은 맨 앞에 넣습니다.
그리고 배열에 저장된 순서대로 i번째 지점 ~ i + 1번째 지점의 거리를 구해주시면 됩니다.
start E L I C E를 인덱스로 0 1 2 3 4 5로 표현한다면
0 1 2 3 4 5에서 각각 인접한 좌표까지의 거리를 구하고,
E의 위치인 1과 5를 바꿔서 0 5 2 3 4 1으로 만들고 각각 인접한 좌표까지의 거리를 다시 구합니다.
위 2가지 방법 중 최솟값으로 답을 구할 수 있습니다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define MAX 1001
using namespace std;
typedef pair<int, int> pii;
int d[MAX][MAX];
int list[MAX][MAX];
int alpha[6][2];
int direct[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };
int N;
void init() {
for (int i = 1; i <= N; i++) {
fill(d[i] + 1, d[i] + 1 + N, 1e9);
}
}
int dijkstra(int sx, int sy, int ex, int ey) {
init();
priority_queue<pair<int, pii>, vector<pair<int, pii> >, greater<pair<int, pii> > > q;
q.push({ 0, {sx,sy} });
d[sx][sy] = 0;
while (!q.empty()) {
int x = q.top().second.first;
int y = q.top().second.second;
int dis = q.top().first;
q.pop();
if (d[x][y] < dis) continue;
for (int i = 0; i < 4; i++) {
int nx = x + direct[i][0];
int ny = y + direct[i][1];
int nextDis = dis + list[x][y] + list[nx][ny];
if (nx < 1 || ny < 1 || nx > N || ny > N) continue;
if (d[nx][ny] <= nextDis) continue;
d[nx][ny] = nextDis;
q.push({ nextDis, {nx,ny} });
}
}
return d[ex][ey];
}
void func() {
int ret = 1e9;
for (int t = 0; t < 2; t++) {
int sum = 0;
for (int i = 0; i < 5; i++) {
sum += dijkstra(alpha[i][0], alpha[i][1], alpha[i + 1][0], alpha[i + 1][1]);
}
ret = min(ret, sum);
swap(alpha[1], alpha[5]);
}
cout << ret << '\n';
}
void input() {
cin >> N;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cin >> list[i][j];
}
}
alpha[0][0] = 1;
alpha[0][1] = 1;
for (int i = 1; i <= 5; i++) {
cin >> alpha[i][0] >> alpha[i][1];
}
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
return 0;
}
|
cs |
'대회 > elice' 카테고리의 다른 글
| 엘리스 코드 챌린지 Day 10 계단 카드 뽑기 (0) | 2024.07.24 |
|---|---|
| 엘리스 코드 챌린지 Day 8 강림제 (0) | 2024.07.23 |
| 엘리스 코드 챌린지 Day 7 계기판 조작하기 (0) | 2024.07.23 |
| 엘리스 코드 챌린지 Day 6 빨간 선과 파란 선 (0) | 2024.07.23 |
| 엘리스 코드 챌린지 Day 5 수열 복원 (0) | 2024.07.22 |