https://www.acmicpc.net/problem/4442

 

처음 주어지는 배열과 다르게 배치된 쌍의 갯수를 구하는 문제로 inversion counting 방식으로 접근할 수 있습니다.

inversion counting이란 순서가 바뀐 순서쌍을 구하는데 사용되는 기법입니다.

즉 자신보다 작지만 뒤에 몇 명이 서있는지 구한다거나 그런 문제들을 이 방식을 사용할 수 있습니다.

 

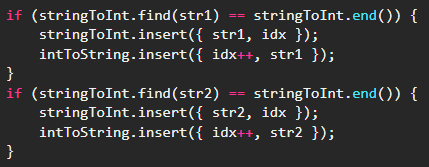
우선 입력이 문자열로 되어있으니 map을 활용하여 첫 번째 배열을 입력받는 순서대로 정수 인덱스로 변경해줍니다.

그 다음 두 번째 배열은 첫 번째 배열에서 구한 인덱스 번호로 변경합니다.

두 번째 입력에서 구한 정수 배열로 트리를 만들도록 합니다.

이 때 트리에 수를 넣어주면서 자신보다 크지만 먼저 들어온 수들의 갯수를 세어주면 됩니다.

배열이 2 3 1 순서대로 저장한다고 가정하면 1을 트리에 넣을때 이미 들어와있던 2, 3을 카운팅 해주는 것입니다.

 

일반적인 map을 사용한 코드의 채점현황입니다.

unordered_map으로 변경한 코드의 채점현황입니다.

이 문제처럼 순서가 중요하지 않고 조회가 많이 발생하는 경우 unordered_map을 사용하는게 더 효율적이라는 것을 알 수 있었습니다.

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <iostream>
#include <unordered_map>
#include <string>
#include <cstring>
#define MAX 100001
using namespace std;
typedef long long ll;
 
unordered_map<string, int> m;
int idxList[MAX];
ll tree[MAX << 2];
int N;
 
void init() {
    m.clear();
    memset(tree, 0, sizeof(tree));
}
 
ll update(int node, int l, int r, int idx, int diff) {
    if (idx < l || r < idx) return tree[node];
    if (l == r) return ++tree[node];
 
    int m = (l + r) >> 1;
    return tree[node] = update(node << 1, l, m, idx, diff) + update((node << 1) + 1, m + 1, r, idx, diff);
}
 
ll query(int node, int l, int r, int s, int e) {
    if (l > e || r < s) return 0LL;
    if (s <= l && r <= e) return tree[node];
 
    int m = (l + r) >> 1;
    return query(node << 1, l, m, s, e) + query((node << 1) + 1, m + 1, r, s, e);
}
 
void func() {
    ll ret = 0LL;
    for (int i = 0; i < N; i++) {
        ret += query(1, 1, N, idxList[i] + 1, N);
        update(1, 1, N, idxList[i], 1);
    }
    cout << ret << '\n';
}
 
void input() {
    cin >> N;
    if (!N) exit(0);
    
    string str;
    int cnt = 0;
    for (int i = 0; i < N; i++) {
        cin >> str;
        m[str] = ++cnt;
    }
 
    for (int i = 0; i < N; i++) {
        cin >> str;
        idxList[i] = m[str];
    }
}
 
int main() {
    cin.tie(nullptr); cout.tie(nullptr);
    ios::sync_with_stdio(false);
 
    while (1) {
        input();
        func();
        init();
    }
 
    return 0;
}
 cs

'algorithm > SegmentTree' 카테고리의 다른 글

boj 8330 순열  (0) 2024.07.21
boj 1517 버블 소트  (0) 2024.06.16
boj 17131 여우가 정보섬에 올라온 이유  (3) 2024.04.25
boj 12895 화려한 마을  (0) 2022.09.07
boj 10167 금광  (0) 2022.09.02

https://www.acmicpc.net/problem/23059

 

23059번: 리그 오브 레게노

첫째 줄에는 백남이가 알고 있는 아이템 사이의 관계의 수 $N$(1 ≤ $N$ ≤ 200,000)를 입력받는다. $N$개의 줄에 걸쳐서 아이템 이름을 의미하는 문자열 2개 A B가 주어진다. 아이템 A는 아이템 B를 구

www.acmicpc.net

간만에 위상정렬 문제입니다.

이 문제는 문자열을 인덱스로 변환해야 하지만 출력하는게 문자열이라 문자열 기준, 인덱스 기준의 맵을 따로 사용하였습니다.

intToString에는 인덱스 기준 문자열, stringToInt에는 문자열 기준 인덱스를 저장합니다.

이 부분이 해당 문자열에 대한 인덱스 값을 구해 맵에 넣는 과정입니다.

stringToInt와 intToString에 같이 넣어줍니다.

그 다음 위상정렬로 구매할 아이템의 순서를 정해주면 되는데

여기서 현재 같은 우선순위의 아이템은 사전 순으로 구매하기 때문에 우선순위를 인덱스로 둔 배열을 사용하였습니다.

우선순위가 낮은 (인덱스가 낮은) 배열부터 문자열들을 사전 순으로 정렬한 후에 출력합니다.

 

이 문제에서 N이 200000이라 MAX를 200000으로 잡았는데.. N이 문자열 갯수가 아닌 관계의 수였습니다..

이런 실수를 좀 줄여야겠습니다..

 

그리고 처음에는 map을 사용했었는데 시간 초과가 발생해서 unordered_map으로 바꾸니 AC를 받았습니다.

찾아보니 데이터가 많을 때 unordered_map의 성능이 훨씬 좋다고 하는 것을 보았습니다.

하지만 이 둘의 차이를 공부할 필요가 있어보입니다.

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <iostream>
#include <unordered_map>
#include <queue>
#include <string>
#include <vector>
#include <algorithm>
#define MAX 400000
using namespace std;
typedef pair<int, int> pi;
 
unordered_map<int, string> intToString;
unordered_map<string, int> stringToInt;
vector<int> graph[MAX], ans[MAX];
int conn[MAX];
int N, idx;
 
bool cmp(int a, int b) {
    return intToString[a] < intToString[b];
}
 
void print() {
    for (int i = 0; ; i++) {
        if (!ans[i].size()) return;
 
        sort(ans[i].begin(), ans[i].end(), cmp);
        for (int j = 0; j < ans[i].size(); j++) {
            cout << intToString[ans[i][j]] << '\n';
        }
    }
}
 
void func() {
    queue<pi> q;
    for (int i = 0; i < idx; i++) {
        if (!conn[i]) {
            q.push({ i,0 });
            ans[0].push_back(i);
        }
    }
 
    for (int t = 0; t < idx; t++) {
        if (q.empty()) {
            cout << "-1\n";
            return;
        }
 
        int x = q.front().first;
        int cnt = q.front().second;
        q.pop();
 
        for (int i = 0; i < graph[x].size(); i++) {
            int next = graph[x][i];
 
            conn[next]--;
 
            if (!conn[next]) {
                q.push({ next, cnt + 1 });
                ans[cnt + 1].push_back(next);
            }
        }
    }
 
    print();
}
 
void input() {
    string str1, str2;
    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> str1 >> str2;
 
        if (stringToInt.find(str1) == stringToInt.end()) {
            stringToInt.insert({ str1, idx });
            intToString.insert({ idx++, str1 });
        }
        if (stringToInt.find(str2) == stringToInt.end()) {
            stringToInt.insert({ str2, idx });
            intToString.insert({ idx++, str2 });
        }
 
        int a = stringToInt[str1];
        int b = stringToInt[str2];
        graph[a].push_back(b);
        conn[b]++;
    }
}
 
int main() {
    cin.tie(NULL); cout.tie(NULL);
    ios::sync_with_stdio(false);
 
    input();
    func();
 
    return 0;
}
 cs

'algorithm > Topological-sort' 카테고리의 다른 글

boj 2252 줄 세우기  (0) 2021.02.07

+ Recent posts

티스토리툴바