https://www.acmicpc.net/problem/17131
17131번: 여우가 정보섬에 올라온 이유
첫 줄에 별의 개수 N이 주어진다. 그 다음 줄부터 N개의 줄에 걸쳐 별의 좌표 x y가 주어진다.
www.acmicpc.net
알고리즘 정말 오랜만이네요.
만들어야 하는 별자리는 V 모양이며, V를 회전한 모양은 포함하지 않습니다. (ex. < > ^ ㄱ ㄴ 모양은 X)
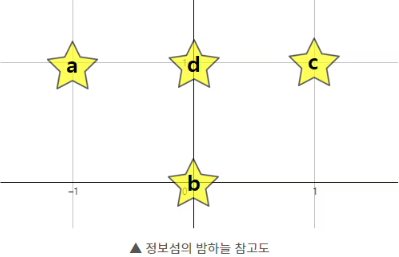
여기서 가로를 x, 세로를 y 축이라고 가정했을 때
예시 기준 a, b, c만 별자리로 인정할 수 있습니다.
그리고 문제에서도 a.x < b.x < c.x이고 a.y > b.y < c.y 라고 친절히 설명도 해줍니다.
이 조건에서 라인 스위핑 기법을 활용하기 위해 y 값 기준 내림차순 정렬이 필요하다는 것을 알 수 있습니다.
그러면 같은 y값들을 가지고 먼저 놓여진 별들 중 x 값이 작은 별들의 갯수와 x 값이 큰 별들의 갯수를 곱하면 별자리의 갯수를 구할 수 있습니다.
어떤 정해진 범위 내에서 특정 범위의 값을 구한다고 했을때 구간합을 떠올릴 수 있습니다.
구간합을 구하는 알고리즘은 세그먼트 트리가 있습니다.
그러면 이 문제는 세그먼트 트리 + 라인 스위핑을 활용하여 해결할 수 있습니다.
로직의 순서는
1. 위에서 설명한것처럼 y 좌표 기준으로 내림차순 정렬합니다.
2. 같은 y값을 가진 별들을 가지고 x 값이 작은/큰 별들의 갯수를 구합니다.
3. 그 다음 같은 y값을 가진 별들을 한꺼번에 트리에 업데이트를 합니다.
이게 끝이지만 주의할점은
같은 y값을 가진 모든 별들이 2번 과정이 끝난 후에 3번 과정을 같이 진행해야합니다.
이 풀이의 핵심은 2번 과정에 들어왔을때 트리에 있는 값들은 모두 자신보다 y 값이 큰 별 이라는 것입니다.
그래서 저는 같은 y값을 가진 별들을 벡터에 넣어주고, 3번 과정에서 한꺼번에 업데이트를 했습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
#include <iostream>
#include <algorithm>
#include <vector>
#define MAX 200001
#define MOD 1000000007
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
ll tree[MAX << 3];
pii list[MAX];
int N;
bool cmp(pii a, pii b) {
if (a.second == b.second) return a.first < b.first;
return a.second > b.second;
}
ll update(int node, int l, int r, int idx) {
if (idx < l || r < idx) return tree[node];
if (l == r) {
return tree[node] = tree[node] + 1;
}
int m = (l + r) >> 1;
return tree[node] = update(node << 1, l, m, idx) + update((node << 1) + 1, m + 1, r, idx);
}
ll query(int node, int l, int r, int s, int e) {
if (s <= l && r <= e) return tree[node];
if (e < l || r < s) return 0LL;
int m = (l + r) >> 1;
return query(node << 1, l, m, s, e) + query((node << 1) + 1, m + 1, r, s, e);
}
void func() {
sort(list + 1, list + 1 + N, cmp);
ll ret = 0;
int pre = list[1].second;
vector<int> v;
for (int i = 1; i <= N; i++) {
int m = list[i].first;
if (pre == list[i].second) {
v.push_back(m);
}
else {
for (auto x : v) {
update(1, 0, (MAX - 1) << 1, x);
}
v.clear();
pre = list[i].second;
v.push_back(m);
}
ret = (ret + query(1, 0, (MAX - 1) << 1, 0, m - 1) * query(1, 0, (MAX - 1) << 1, m + 1, (MAX - 1) << 1)) % MOD;
}
cout << ret << '\n';
}
void input() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> list[i].first >> list[i].second;
list[i].first += (MAX - 1);
}
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
return 0;
}
|
cs |
'algorithm > SegmentTree' 카테고리의 다른 글
| boj 8330 순열 (0) | 2024.07.21 |
|---|---|
| boj 1517 버블 소트 (0) | 2024.06.16 |
| boj 12895 화려한 마을 (0) | 2022.09.07 |
| boj 10167 금광 (0) | 2022.09.02 |
| boj 16993 연속합과 쿼리 (0) | 2022.08.29 |